所有资料来源于网络,仅供大家参考学习
河北2019年单招理科数学模拟试题系列一【含答案】
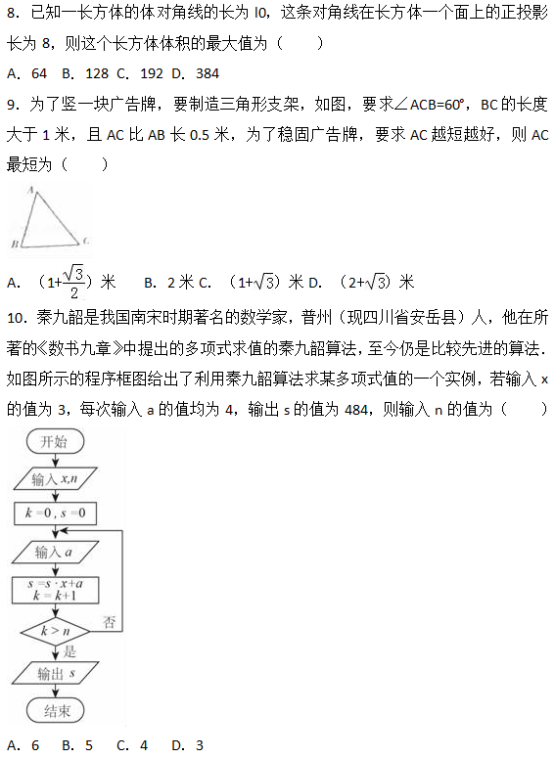
一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.




二.填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡相应的横线上.

三、解答题:(共5小题,共70分;要求写出必要的文字说明,解题过程和演算步骤)
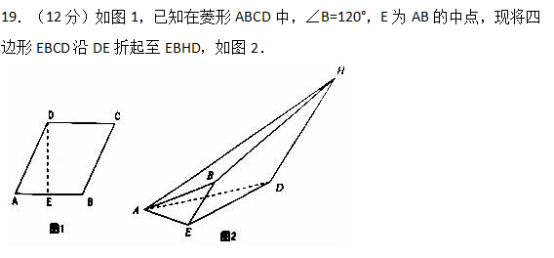
 18.(12分)某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.
18.(12分)某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.
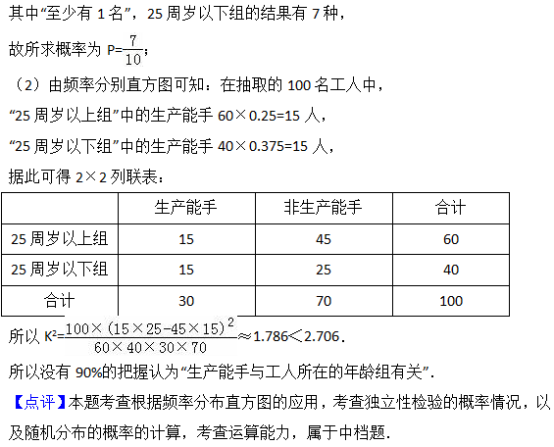
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90% 的把握认为“生产能手与工人所在的年龄组有关”?

附:x2= P(x2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
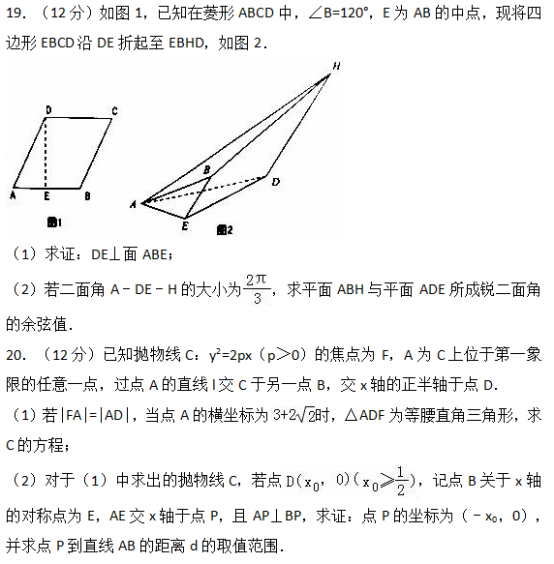

[选修4-4:坐标系与参数方程]

[选修4-5:不等式选讲]
河北2019年单招理科数学模拟试题系列一参考答案
一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.








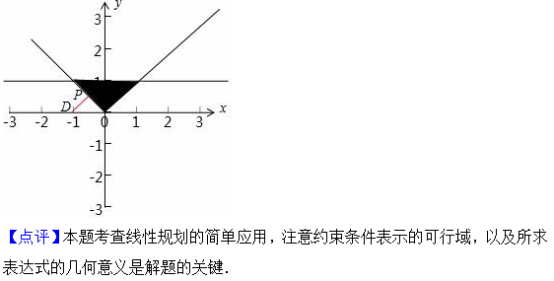




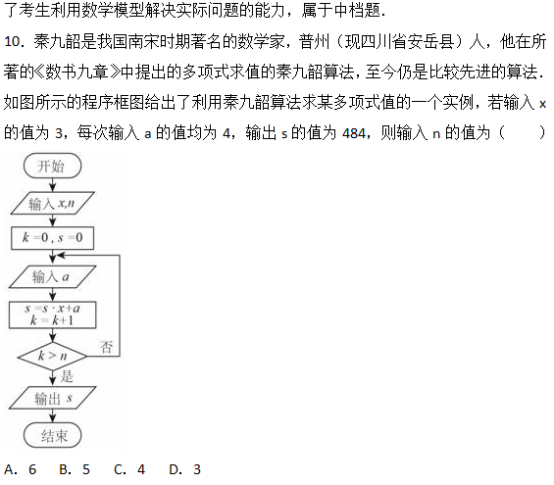



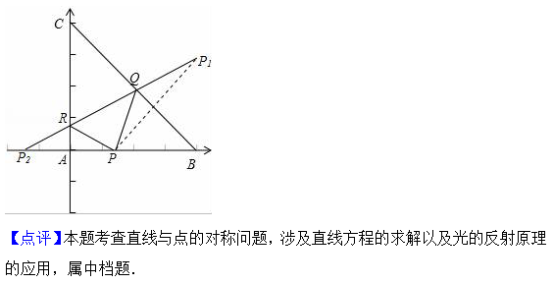




二.填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡相应的横线上.


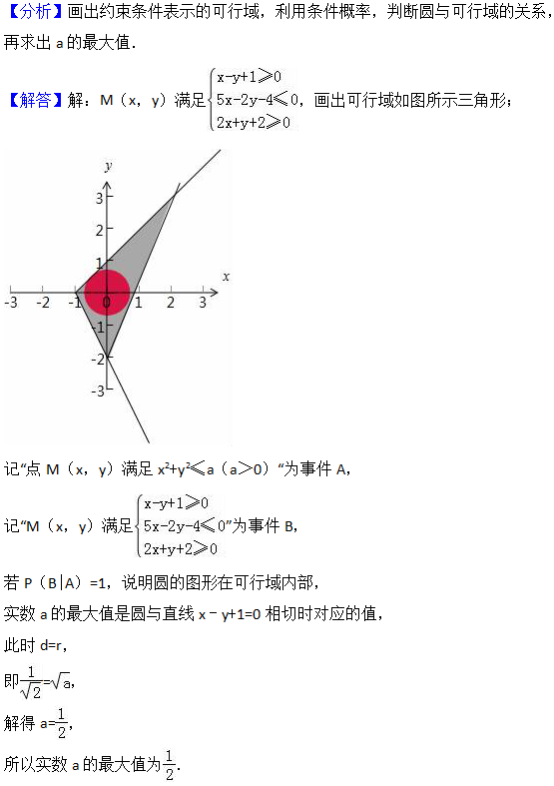




三、解答题:(共5小题,共70分;要求写出必要的文字说明,解题过程和演算步骤)


18.(12分)某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90% 的把握认为“生产能手与工人所在的年龄组有关”?
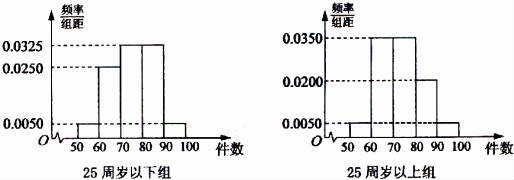
附:x2= P(x2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
【考点】BO:独立性检验的应用.
【分析】(1)根据分层抽样,求得样本中有25周岁以上组工人60名,25周岁以下组工人40人,由频率分布直方图日平均生产件数不足60件的工人中25周岁以上组有3人,25周岁以下组有2人,随机抽取2人,求得所有可能的结果,根据古典概型公式求得至少抽到一名“25周岁以下组”工人的概率;
(2)据2×2列联表,代入求临界值的公式,求出观测值,利用观测值同临界值表进行比较,K2≈1.786<2.706,没有90%的把握认为“生产能手与工人所在的年龄组有关”.
【解答】解:(1)由已知得:样本中有25周岁以上组工人60名,25周岁以下组工人40人,
所以样本中日平均生产件数不足60件的工人中25周岁以上组有60×0.05=3人,分别记为:A1,A2,A3,
25周岁以下组有工人40×0.05=2人,分别记为B1,B2,
从中随机抽取2人,所有可能的结果共10种,他们分别是(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B2),(A3,B2),(B1,B2),








[选修4-4:坐标系与参数方程]



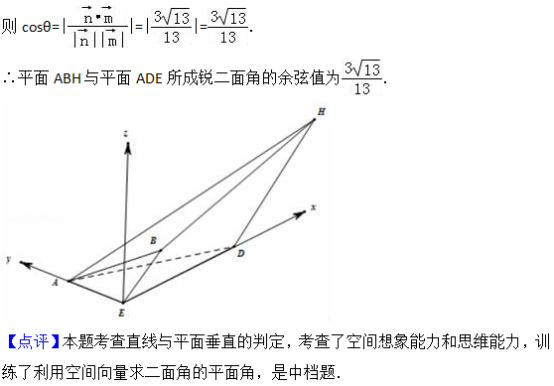
【点评】本题考查直线与曲线的极坐标方程的求法,考查三角形的面积的求法,考查参数方程、直角坐标方程的互化、三角函数性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.
[选修4-5:不等式选讲]



所有资料来源于网络,仅供大家参考学习

很多人想知道河北有哪些比较好的单招学校,具体排名情况是怎样的呢?下面小编为大家介绍一下比较好的河北单招学校名单院校名字推荐指数邢台职业技术学...

一般高职专科自主招生分数线在200分左右能通过,下面小编为大家详细介绍一下2019河北高职专科自主招生多少分及格,供参考!2019河北高职专...

很多人想知道河北有哪些比较好的单招学校,具体排名情况是怎么样的呢?下面小编为大家整理了2019河北十大单招学校排名名单,供参考!2019河北...

很多人想知道河北有哪些单招学校,具体排名情况是怎样的呢?下面小编为大家整理了河北高职单招学校名单,供参考!2019河北高职单招学校具体名单汇...

2018年河北单招一般多少分能过?这是众多想考河北单招的同学共同的问题,因为这样有利于我们根据分数要求提高自己,达到相应的分数,并努力进入自...

河北单招学校哪个最好?有途高考网小编整理了2018年河北最好的十大高职单招院校排名,供大家在报名选择专业院校时作参考,单招院校排名每年都会有...

目前各省单招正在进行中,准备河北高职单招考试的同学们有没有想好自己打算报考哪所单招学校?河北有哪些比较好的公办单招院校?下文有途网小编给大家...

2018年的河北单招即将开始,有很多想去河北单招的同学,小编这里有一些关于2018河北单招院校的名单,希望对参加河北单招的你有些帮助。【一】...

2018年高职单招考试已经陆续开始进行了,想要参加高职单招考试的考生们需要注意了,2018河北高职单招有哪些公办院校,下文是有途网小编整理的...

参加2017年秦皇岛职业技术学院高职单招考试的考生注意啦!!!有途网小编为您整理了秦皇岛职业技术学院2017年单招专业及计划表,供您参考,希...

高职单招考试的报名正在进行中,有很多同学问小编石家庄地区都有什么学校在进行高职单招招生。下面就是有途网小编为准备报考石家庄地区的考生搜集的石...