2017年齐齐哈尔市中考数学试题
第Ⅰ卷(共30分)
一、2017年齐齐哈尔市中考数学试题选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.![]() 的绝对值是( )
的绝对值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列四个图形分别是节能、节水、低碳和绿色食品标志,是轴对称图形的是( )

3.作为“一带一路”倡议的重大先行项目,中国、巴基斯坦经济走廊建设进展快、成效显著.两年来,已有18个项目在建或建成,总投资额达185亿美元.185亿用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列算式运算结果正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买( )
A.16个 B.17个 C.33个 D.34个
6.若关于![]() 的方程
的方程![]() 有实数根,则实数
有实数根,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() 或
或![]() C.
C.![]() D.
D.![]()
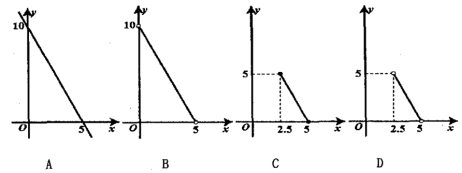
7.已知等腰三角形的周长是10,底边长![]() 是腰长
是腰长![]() 的函数,则下列函数中,能正确反映
的函数,则下列函数中,能正确反映![]() 与
与![]() 之间函数关系的图象是( )
之间函数关系的图象是( )
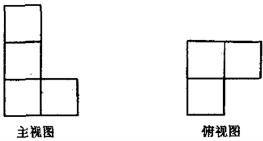
8.一个几何体的主视图和俯视图如图所示,若这个几何体最多有![]() 个小正方体组成,最少有
个小正方体组成,最少有![]() 个小正方体组成,则
个小正方体组成,则![]() 等于( )
等于( )
A.10 B.11 C.12 D.13
9.一个圆锥的侧面积是底面积的3倍,则圆锥侧面展开图的扇形的圆心角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
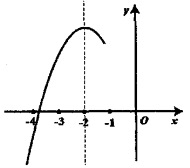
10.如图,抛物线![]() (
(![]() )的对称轴为直线
)的对称轴为直线![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:①
之间,其部分图象如图所示,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤点
为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ,正确的个数有( )
,正确的个数有( )
A.4个 B.3个 C.2个 D.1个
第Ⅱ卷(共90分)
二、2017年齐齐哈尔市中考数学试题填空题填空题(每题3分,满分27分,将答案填在答题纸上)
11.在某次七年级期末测试中,甲、乙两个班的数学平均成绩都是89.5分,且方差分别为![]() ,
,![]() ,则成绩比较稳定的是 班.
,则成绩比较稳定的是 班.
12.在函数![]() 中,自变量
中,自变量![]() 的取值范围是 .
的取值范围是 .
13.矩形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,请你添加一个适当的条件 ,使其成为正方形(只填一个即可).
,请你添加一个适当的条件 ,使其成为正方形(只填一个即可).
14.因式分解:![]() .
.
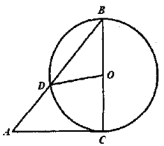
15.如图,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的度数为 .
的度数为 .
16.如图,在等腰三角形纸片![]() 中,
中,![]() ,
,![]() ,沿底边
,沿底边![]() 上的高
上的高![]() 剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是 .
剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是 .
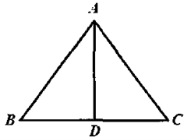
17.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段![]() 是
是![]() 的“和谐分割线”,
的“和谐分割线”,![]() 为等腰三角形,
为等腰三角形,![]() 和
和![]() 相似,
相似,![]() ,则
,则![]() 的度数为 .
的度数为 .
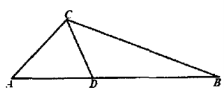
18.如图,菱形![]() 的一边
的一边![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() 是坐标原点,
是坐标原点,![]() ,反比例函数
,反比例函数![]() 的图像经过点
的图像经过点![]() ,与
,与![]() 交于点
交于点![]() ,若
,若![]() 的面积为20,则
的面积为20,则![]() 的值等于 .
的值等于 .
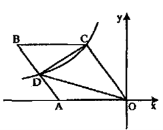
19.如图,在平面直角坐标系中,等腰直角三角形![]() 的直角边
的直角边![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() ,以
,以![]() 为直角边作第二个等腰直角三角形
为直角边作第二个等腰直角三角形![]() ,以
,以![]() 为直角边作第三个等腰直角三角形
为直角边作第三个等腰直角三角形![]() ,则点
,则点![]() 的坐标为 .
的坐标为 .

三、2017年齐齐哈尔市中考数学试题解答题 (本大题共6小题,共63分.解答应写出文字说明、证明过程或演算步骤.)
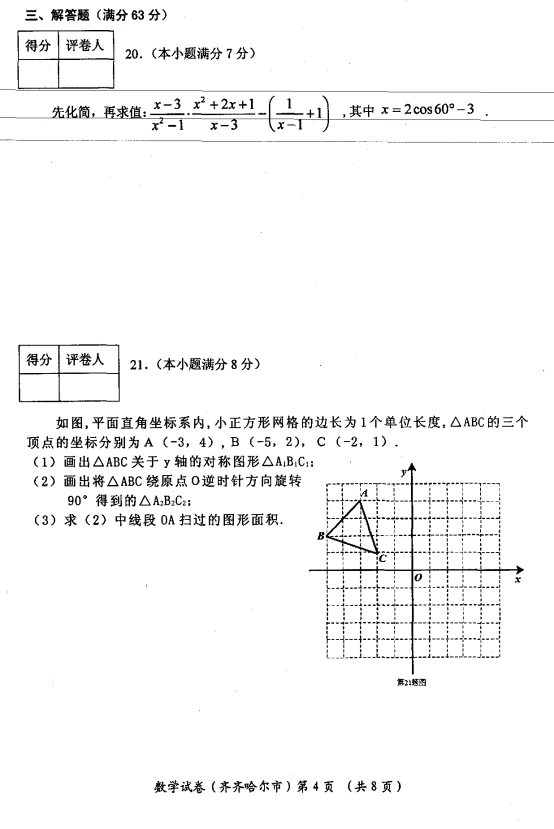
20.先化简,再求值:![]() ,其中
,其中![]() .
.
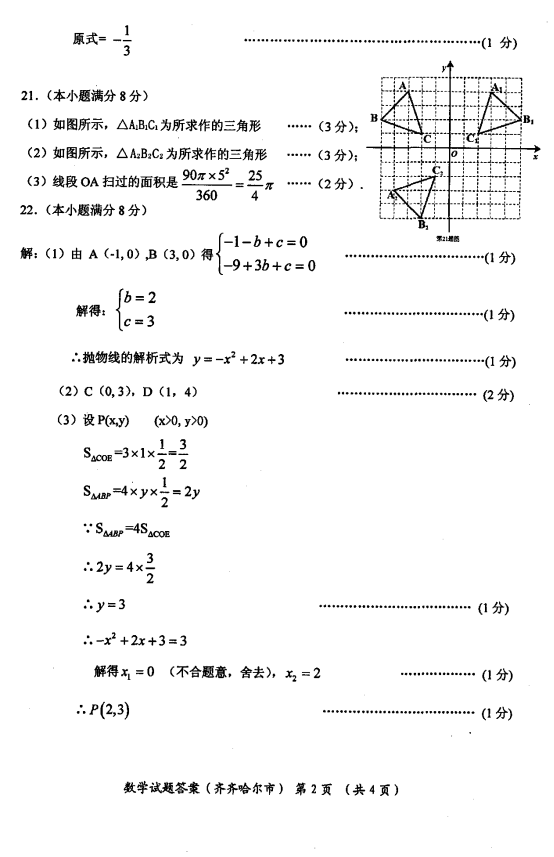
21.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
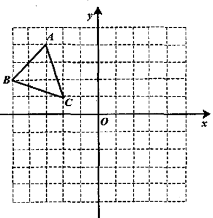
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ;
;
(2)画出将![]() 绕原点
绕原点![]() 逆时针方向旋转
逆时针方向旋转![]() 得到的
得到的![]() ;
;
(3)求(2)中线段![]() 扫过的图形面积.
扫过的图形面积.
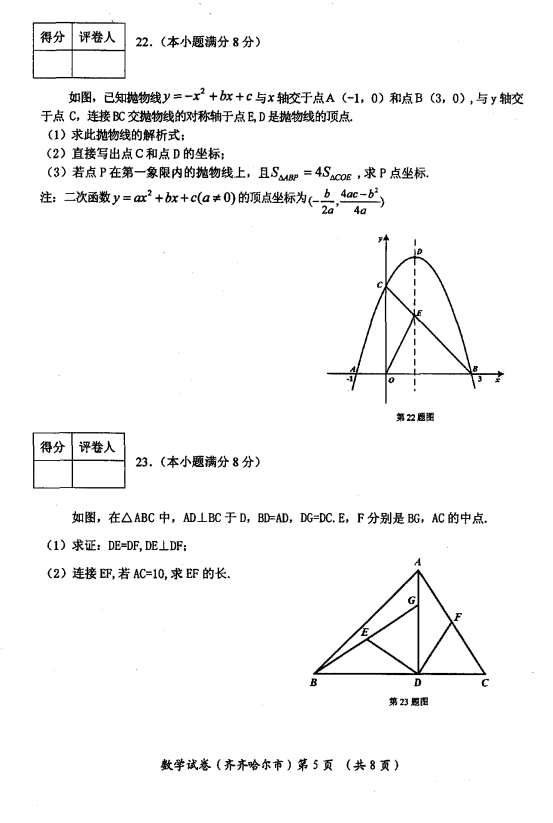
22.如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,
,![]() 是抛物线的顶点.
是抛物线的顶点.
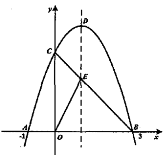
(1)求此抛物线的解析式;
(2)直接写出点![]() 和点
和点![]() 的坐标;
的坐标;
(3)若点![]() 在第一象限内的抛物线上,且
在第一象限内的抛物线上,且![]() ,求
,求![]() 点坐标.
点坐标.
注:二次函数![]() (
(![]() )的顶点坐标为
)的顶点坐标为![]() .
.
23.如图,在![]() 中,
中,![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
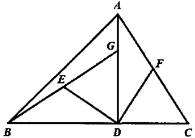
(1)求证:![]() ,
,![]() ;
;
(2)连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
24.为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出不完整的频数分布表和频数分布直方图.请根据图表信息解答问题:
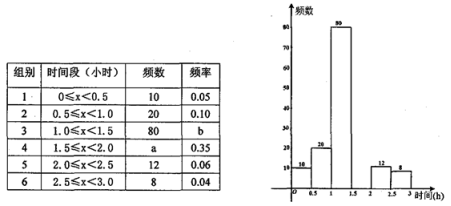
(1)表中![]() ,
,![]() ;
;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第 组;
(4)请估计该校七年级学生日阅读量不足1小时的人数.
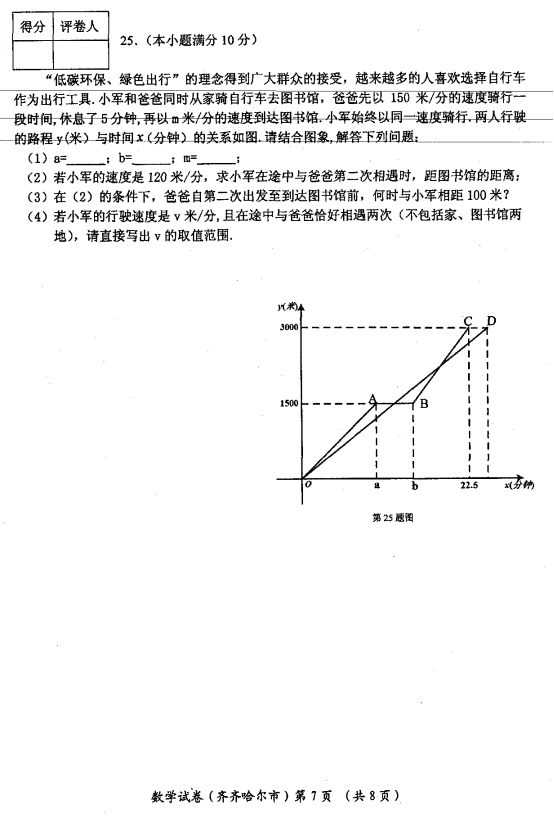
25.“低碳环保、绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以![]() 米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程
米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程![]() (米)与时间
(米)与时间![]() (分钟)的关系如图.请结合图象,解答下列问题:
(分钟)的关系如图.请结合图象,解答下列问题:
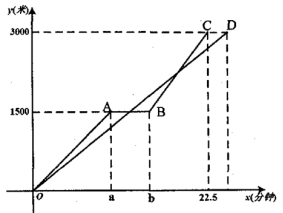
(1)![]() ;
;![]() ;
;![]() ;
;
(2)若小军的速度是120米/分,求小军在图中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是![]() 米/分,且在图中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在图中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出![]() 的取值范围.
的取值范围.
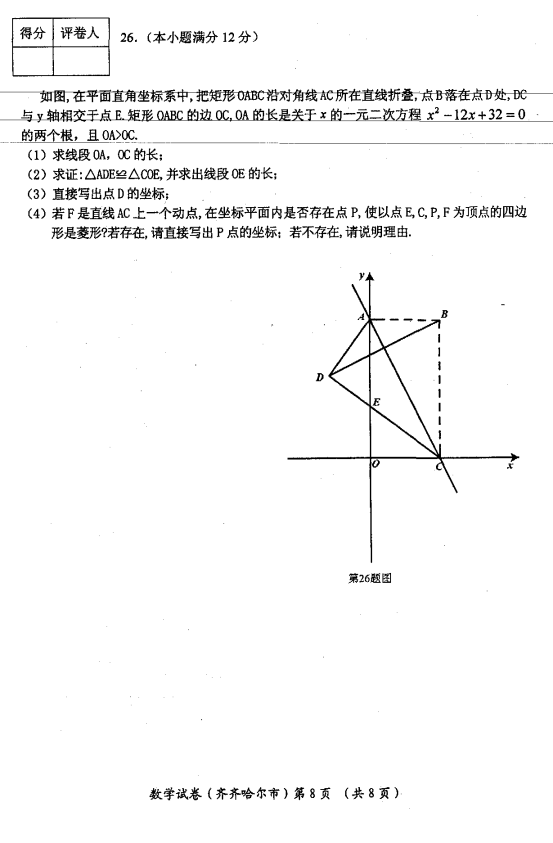
26.如图,在平面直角坐标系中,把矩形![]() 沿对角线
沿对角线![]() 所在的直线折叠,点
所在的直线折叠,点![]() 落在点
落在点![]() 处,
处,![]() 与
与![]() 轴相交于点
轴相交于点![]() .矩形
.矩形![]() 的边
的边![]() ,
,![]() 的长是关于
的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,且
的两个根,且![]() .
.

(1)求线段![]() ,
,![]() 的长;
的长;
(2)求证:![]() ,并求出线段
,并求出线段![]() 的长;
的长;
(3)直接写出点![]() 的坐标;
的坐标;
(4)若![]() 是直线
是直线![]() 上一个动点,在坐标平面内是否存在点
上一个动点,在坐标平面内是否存在点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形?若存在,请直接写出
为顶点的四边形是菱形?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.







![]()

2019年转眼间就要过去一半了,高中生们即将迎来期待的暑期生活。下文有途网小编给大家整理了2019年黑龙江高中生的暑假放假时安排,供参考!黑...

2019中考在即,各省市的中考时间都不是统一规定的,下文有途网小编给大家整理了2019黑龙江各市的中考时间安排在什么时候,以及中考的考试科目...

2017年中考结束了。各位家长以及同学最关心的问题就是想要报名的高中的录取分数线是多少,现在有途网小编来告诉大家肇东一中的录取分数线。201...

2017年龙东六市中考数学试题word版(含答案)

2017年绥化市中考语文试题word版(含答案)

中考过后,同学们最关心的就是自己分数能够上哪些高中,下面是由有途网小编指南整理的绥化市的部分高中分数预测,仅供参考,具体以官网公布为准。希望...

中考过后,同学们最关心的就是自己分数能够上哪些高中,下面是由有途网小编指南整理的双鸭山市的部分高中分数预测,仅供参考,具体以官网公布为准。希...

中考过后,同学们最关心的就是自己分数能够上哪些高中,下面是由有途网小编指南整理的伊春市的部分高中分数预测,仅供参考,具体以官网公布为准。希望...

中考过后,同学们最关心的就是自己分数能够上哪些高中,下面是由有途网小编指南整理的佳木斯市的部分高中分数预测,仅供参考,具体以官网公布为准。希...

中考过后,同学们最关心的就是自己分数能够上哪些高中,下面是由有途网小编指南整理的牡丹江市的部分高中分数预测,仅供参考,具体以官网公布为准。希...

中考过后,同学们最关心的就是自己分数能够上哪些高中,下面是由有途网小编指南整理的哈尔滨市的部分高中分数预测,仅供参考,具体以官网公布为准。希...

2017中考即将到来,中考是检测初中在校生是否达到初中学业水平的水平性考试和建立在九年义务教育基础上的高中选拔性考试;是初中毕业证发放的必要...

九年寒窗,一朝及第。中考成绩一分一操场的情况已成定局。考生应抱有每分必争,尽量不失分的原则参加考试。下面是由有途网整理的2017年绥化市中考...

九年寒窗,一朝及第。中考成绩一分一操场的情况已成定局。考生应抱有每分必争,尽量不失分的原则参加考试。下面是由有途网整理的2017年齐齐哈尔市...